Terms that appear frequently throughout this lesson are defined below:
| Term | Definition |
| Correlation | A statistical relationship that reflects the association between two variables |
|
Pearson correlation coefficient |
A number (rp) that represents the strength of the association/correlation between two variables |
|
Spearman correlation coefficient |
The nonparametric equivalent (rs) of the Pearson correlation coefficient |
| Multiple regression | Using two or more independent variables to predict a dependent variable |
|
Unstandardized regression coefficient (b) |
The change in the dependent variable associated with a 1 unit change in the independent variable when all other variables in the regression model are controlled for |
|
Standardized regression coefficient (beta) |
Each variable is transformed to have a mean of 0 and standard deviation of 1 so that the regression coefficients represent how predictive the variable is (i.e., the magnitude of the coefficients can be compared to one another to determine which is most predictive of the outcome) |
|
R2 |
The amount of variance in the data accounted for by a regression model |
| Statistical control | Separating out the effect of one independent variable from the remaining independent variables to reduce the effect of confounding |
| Confounding variable | An extraneous variable that correlates with the dependent variable and at least one independent variable |
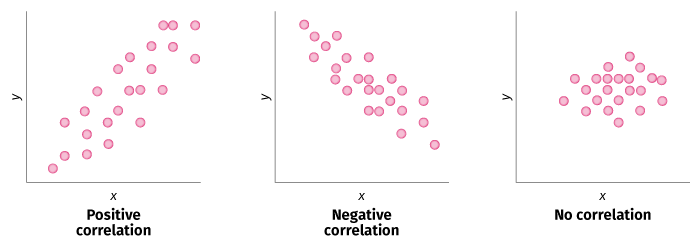
A correlation reflects the association between two variables. It tells us a) the strength of the relationship, on a scale of 0 to +/-1 with 0 indicating a lack of association and b) the direction of the relationship, either positive (i.e., as one variable increases the other increases) or negative (i.e., as one variable increases the other decreases).
Pearson correlation coefficient (also known as the Pearson product moment correlation coefficient and simple correlation coefficient) provides a value for r that indicates the strength and direction of the relationship between two variables.
Spearman’s coefficient is the nonparametric equivalent of the Pearson correlation coefficient and is typically applied to data that do not meet the assumption of normality.
For Example
Large cities often see increases in violent crime and ice cream sales during the summer. Does ice cream cause violent crime? Not necessarily (whew!)…possible explanations include:
Multiple regression is used to predict an outcome based on two or more independent variables. Multiple regression expresses the relationship between the variables in the form of a linear equation. The equation for the regression line generally follows the form:
y = b0 +b1x1 +b2x2+…..bnxn where:
Click here for a detailed description.
The unstandardized regression coefficient represents the measurement unit (e.g., pounds, liters, years) associated with its independent variable. For example, in a single regression equation, one independent variable may be measured in years while another is measured in pounds. This makes comparisons about the predictive ability of the independent variables difficult, since the measurement units vary.
To make comparisons across independent variables, researchers often use standardized regression coefficients, or beta-weights. To calculate beta-weights, each variable is converted to have a mean of 0 and standard deviation of 1, resulting in coefficients that can be compared directly to one another. This enables the researcher to determine the relative effect of each independent variable in the regression model.
Regression coefficients provide information about how each independent variable impacts the dependent variable. One condition of interpreting a single regression coefficient is “controlling for all other variables.” This means that all other independent variables are held constant for calculations made about the effect of the independent variable on the dependent variable.
Variables that distort the observed relationship between the dependent variable and independent variable of interest are called confounders. In regression, confounders should be entered into the model in order to “adjust” for those variables, since we know or believe that they impact the dependent variable.
R2 (also called coefficient of determination) is the percentage of variance in the data explained by your regression model. In other words, it is a measure of how close the data from your sample are fitted to the regression line.
Methods: Sixty participants were recruited from four continuing care retirement communities, providing services and approximately 400 apartments (some >1 resident) to adults aged 55 years and older. Means and standard deviations were calculated on all variables. All variables were normally distributed (mean skewness and kurtosis values greater than -1.0 and less than +1.0), with the exception of percent active time in high intensity activity which was positively skewed (skewness = 2.24) and leptokurtic (kurtosis = 5.59). Relationships between indices of stepping behavior (i.e., total steps/day, percent active time in moderate and high intensity activity) and self-efficacy for exercise, overcoming barriers self-efficacy, trait anxiety, and fear of falling were examined using Pearson’s product moment correlation.
| Steps Per Day | Moderate-Intensity PA | High-Intensity PA | Exercise Self-Efficacy | Barriers Self-Efficacy | Trait Anxiety | Fear of Falling | |
|---|---|---|---|---|---|---|---|
| Steps per day | – | ||||||
| Moderate-intensity PA | 0.600° | – | |||||
| High-intensity PA | 0.459° | 0.126 | – | ||||
| Exercise self-efficacy | 0.367° | 0.264 | 0.151 | – | |||
| Barriers | 0.265 | 0.077 | 0.298*† | 0.617° | – | ||
| Trait anxiety | 0.206 | 0.292* | -0.125 | -0.171 | -0.231 | – | |
| Fear of falling | 0.080 | 0.120 | -0.006 | -0.163 | -0.021 | -0.001 | – |
Results: Correlations among total number of steps per day, percent of active time in moderate and high intensity physical activity, exercise self-efficacy, overcoming barriers self-efficacy, trait anxiety, and fear of falling and are presented in Table 3. Exercise self-efficacy was the only variable that significantly correlated with total number of steps per day (r = 0.367, p = 0.009). Overcoming barriers self-efficacy was the only variable significantly correlated with percentage of time spent in high intensity physical activity (r = 0.298, p = 0.044). Fear of falling was not significantly related to total steps per day, moderate intensity physical activity, or high intensity physical activity behavior.
Methods: Multiple regression was used to evaluate the relationship between adherence and glycemic control by means of a backward elimination process. Several patient-related and provider-related factors were used as covariates in the model for statistical adjustment, including original ODM regimen, baseline A1C, sex, age at index date, CDS, and medication burden, as well as provider sex, specialty, and years since medical school graduation.
Click here for a detailed description.
Results: Multiple regression was used to determine the relationship between adherence and A1C, controlling for therapeutic regimen and baseline A1C. An inverse relationship was observed between ODM adherence and A1C (see figure above), in which a 10% increase in index ODM adherence was associated with a 0.1% decrease in A1C (p = .0004).
Methods:Performance on the HSRT was compared with data collected during the admissions process, including gender, presence of a four-year degree, undergraduate GPA, PCAT composite percentile rank, PCAT chemistry percentile rank, PCAT quantitative percentile rank, PCAT biology percentile rank, PCAT verbal percentile rank, and PCAT reading comprehension percentile rank. Multiple linear regression was conducted using SAS (SAS Institute, Inc., Cary, NC) to assess the relationship between predictor variables and HSRT scores after controlling for other variables.
Linear Regression Model Predicting HSRT Scores
| Variable | Unstandardized Regression Coefficient | P Value |
|---|---|---|
| Prior 4-year degree | -0.52 | 0.15 |
| Undergraduate GPA | 0.96 | 0.10 |
| Reading comprehension PCAT score | 0.05 | <0.001 |
| Verbal PCAT score | 0.06 | <0.001 |
| Quantitative PCAT score | 0.05 | <0.001 |
| Chemistry PCAT score | -0.02 | 0.05 |
| Biology PCAT score | -0.01 | 0.38 |
Results: The table above presents the results of multivariate analyses predicting HSRT scores. The full model explained 27.4% of the variance in HSRT scores. After controlling for other predictors, three variables were significantly associated with HSRT scores: scores on the reading comprehension, verbal, and quantitative sections of the PCAT.