Lesson 2: Descriptive Statistics

A sample is the subset or group (e.g., individuals, cells, animals, machines) drawn from the population for data collection. Descriptive statistics describe the sample from which data is collected and communicate the results without attempting to generalize beyond the individuals included in the sample. The goal of inferential statistics is to determine the likelihood that the observed results can be generalized to other samples.

Descriptive statistics represent large amounts of data in an aggregate form. There are three basic descriptive characteristics for a single variable:

1. Central tendency: An estimate of the “center” of a distribution of values for continuous variables.
   1. The mean, or average, is calculated by adding up all the values and dividing by the number of the values.
   2. The median is the value found in the exact middle of the set of values. If there are an even number of values and the middle values differ, the median is interpolated.
   3. The mode is the most frequently occurring value.
2. Dispersion: Represents the spread of the data round the measure of central tendency.
   1. The standard deviation (SD) shows the relation of the values to the mean and is most commonly reported with the mean. It is the square root of the variance, which is calculated by summing the squares of the difference between each value and the mean and dividing the sum of squares by the number of values minus 1. Large standard deviations suggest that the data are generally spread out far from the mean. Small standard deviations suggest that the values are tightly clustered around the mean.
   2. The range is the difference between the highest value and the lowest value. Note that it is sensitive to outliers, as an outlier can greatly exaggerate the range.
   3. The interquartile range (IQR), also called middle fifty or midspread, is the difference between the first quartile and the third quartile of the data. The median is the corresponding measure of central tendency.

   Consider These Numbers	Mean, SD	Median, Range	Mode	IQR
   2, 4, 5, 6, 7, 1, 3, 5, 4 ,3, 2, 2	3.7, 1.8	3.5, 6	2	3
   10, 14, 34, 25, 92, 34, 54, 20, 34	35.2, 25.0	34, 82	34	27
   6, 6, 7, 5, 7, 5, 4, 6, 8, 6	6.0, 1.2	6, 4	6	2

3. Frequency distribution: Summary of the frequency of individual values or ranges of values for a variable. Frequency distributions are usually represented in one of two ways: as a table or as a graph.

   

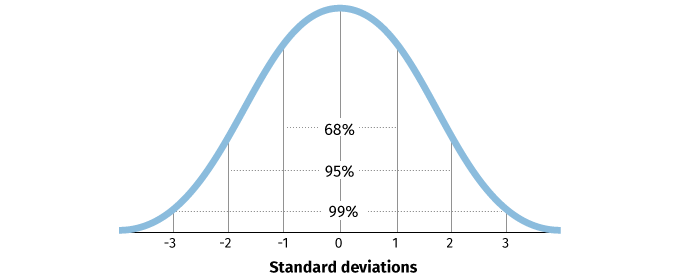
   1. Normal distribution: The Gaussian or bell curve, in which 50% of the values occur above and below the mean, 68% of values fall within 1 standard deviation, 95% of values fall within 2 standard deviations, 99% of the values fall within 3 standard deviations, and the mean = median = mode.
   2. Binomial distribution: The probability distribution for a binomial variable that is tested in repeated trials (e.g., flipping a coin for heads/tails 100 times); fixed probabilities add up to one.
   3. Confidence Interval: Provides an estimated range of values in which the population parameter is likely to fall a specified proportion of the time, typically either 95% or 99% of the time. In other words, a 95% confidence interval means that the confidence interval should contain the population parameter 95 times if the study is repeated 100 times.

When descriptive data is computed, the following guidelines are generally followed:

Example 1: Patient Characteristics

In the following table, mean and standard deviation are reported for continuous variables (e.g., age, number of medications per patient) and frequency for nominal (e.g., gender, ethnicity, race) and ordinal variables (e.g., number of past pharmacist-managed clinic visits):

Patient Demographics

*Total is greater than 100% due to patients having multiple pharmacist-managed disease states>

Example 2: Survey Responses

The following table reports the median and range for ordinal data measured on a Likert scale survey. This table also reports the totals for each response, which provides the frequency distribution for each of the Reasons:

Ranking of the Importance of the Reasons/Motivation to Study Pharmacy
(ranked on 5 Likert scale ranging from 1=not important to 5=very important)

Example 3: Periodontitis

The following figure represents a simple frequency distribution for the age of periodontitis patients, showing two peaks:

A box plot diagram is a more robust approach to graphically representing the frequency distribution, along with central tendency and dispersion. The box plot below shows age distribution by gender in patients with chronic periodontitis and aggressive periodontitis. The box encompasses the interquartile range and the black line represents the median. The median was lower for patients with aggressive periodontitis than those with chronic periodontitis. Higher variability of age among females with aggressive periodontitis and lower variability among males in the same group were observed. Several outliers were observed in the aggressive form, as indicated by the stars and circles (i.e., data points that did not fall within the whiskers):